Сложение и вычитание смешанных чисел. Часть 1 (5 класс).
Тему «Сложение и вычитание смешанных чисел» рассмотрим в два этапа для более лучшего восприятия. В данной статье рассмотрим как складываются и вычитаются смешанные числа с дробной частью, которая имеет дроби с одинаковыми знаменателями (как правило, данная тема изучается в 5 классе). Как складываются смешанные числа с дробной частью, имеющей дроби с разными знаменателями, рассмотрим отдельно, в другой статье (изучается в 6 классе). Все правила наизусть!!! Тема не сложная, но напрячься чуть надо… Ну что, набираемся терпенья и поехали…
Для сложения данных смешанных чисел действует следующее правило.
Правило. При сложении (вычитании) смешанных чисел целые части складываем (вычитаем) отдельно, а дробные отдельно. (Т.е. «целые с целыми», «дробные с дробными»).
Как применяется правило?
Рассмотрим пример на сложение.
Выполнить действие.
Решение.
Определяем, где целые и где дробные части. Целые части — это 5 и 3, дробные части — это 
. А дальше начинаем складывать по правилу: целые с целыми, дробные с дробными. Как сложить целые числа, думаю, проблем не возникнет. Сложение дробных частей представляет собой сложение дробей с одинаковыми знаменателями, для тех, кто не знает как выполнить такое сложение можно посмотреть здесь. Т.е.
Следуя рекомендации по записи ответа (рекомендации можно посмотреть здесь), получаем: дробь не сокращается, выделять целую часть из дробной не надо, поэтому полученное число число пойдет в ответ.
На первых этапах решения таких примеров лучше все расписывать, после, когда уже «рука набьется», можно записывать короче: 
Рассмотрим примеры на вычитание.
Случай I. Дробная часть уменьшаемого больше дробной части вычитаемого
Рассмотрим следующий пример.
Выполнить действие.
Решение.
Начинаем решение примера с определения целых и дробных частей. Целые части — это 6 и 3, дробные части это 
. А дальше начинаем вычитать по правилу. Как вычитать целые числа, думаю, проблем не возникнет. Вычитание дробных частей представляет собой вычитание дробей с одинаковыми знаменателями, для тех, кто не знает как выполнить такое сложение можно посмотреть здесь. Т.е.
Не забываем про рекомендации по записи ответа (рекомендации можно посмотреть здесь), получаем: дробь не сокращается, выделять целую часть из дробной не надо, поэтому полученное число пойдет в ответ.
На первых этапах решения таких примеров лучше все расписывать, после, когда уже «рука набьется», можно записывать короче:
Случай II. Дробная часть уменьшаемого меньше дробной части вычитаемого.
При решении примеров на вычитание смешанных чисел может встретиться случай, когда дробная часть уменьшаемого меньше дробной части вычитаемого. Как поступать в этом случае?
Рассмотрим на примере.
Выполните действие.
Решение.
Смотрим на пример и видим, что перед нами вычитание смешанных чисел. Как обычно поступаем со сложением (вычитанием) смешанных чисел: «складываем (вычитаем) целое с целым, дробное с дробным». Но не тут — то было: (7-3) – сможем вычесть, а вот из 
— не сможем. Как поступить с вычитанием дробных частей? Рассуждаем. Когда мы сможем вычесть? Когда первая дробь будет больше второй, поэтому наша задача состоит в том, чтобы увеличить первую дробь. Каким же образом будем увеличивать? Очень просто, будем у 7 «забирать» единицу и добавлять ее к дроби и затем «превратим» ее в неправильную… Ну что, поехали…
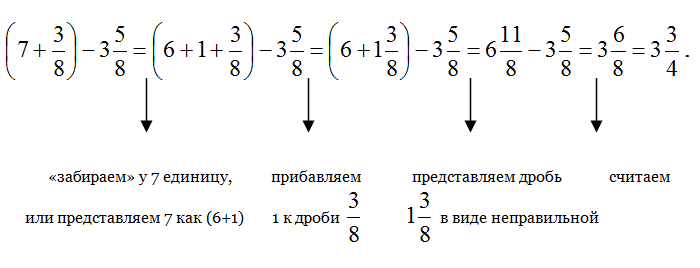
Следуя рекомендации по записи ответа (рекомендации можно посмотреть здесь), получаем: дробь не сокращается, выделять целую часть из дробной не надо, поэтому полученное число пойдет в ответ.
Случай III. Вычитание дроби из натурального числа, смешанного числа из натурального.
Что же делаем в данном случае, когда будем вычитать дробь из натурального числа, и если будем вычитать смешанное число из натурального числа.
Рассмотрим примеры.
Выполнить действие.
Решение.
В данном примере надо выполнить действие на вычитание дроби из целого числа. Что же делаем? У 3 «забираем» единицу, почему же единицу, чем она хороша в данном случае? Да потому, что ее можно представить в виде дроби с одинаковым числителем и знаменателем, т.е. 
и т.д.
В нашем случае будем ориентироваться на дробь 
, точнее на ее знаменатель. У нее знаменатель равен 8, тогда и нашу 1 будем представлять в виде дроби 
. А далее выполняем нужное нам действие: вычитание смешанных чисел.
Следуя рекомендации по записи ответа (рекомендации можно посмотреть здесь), получаем: дробь не сокращается, выделять целую часть из дробной не надо, поэтому полученное число пойдет в ответ.
Таким же образом поступаем и в следующем примере на вычитание смешанного числа из целого.
Выполнить действие.
Решение.
Не забываем про рекомендации по записи ответа (рекомендации можно посмотреть здесь), получаем: дробь не сокращается, выделять целую часть из дробной не надо, поэтому полученное число пойдет в ответ.
Что осталось сделать по данной теме, так это отработать навыки решения.
Большую проблему вызывает вычитание смешанных чисел. Поэтому, у кого есть вопросы, смотрим внимательно видео и пытаемся разобраться. Рекомендую посмотреть разбор всех примеров, каждый из которых хорош по — своему.
P.S. Есть второй способ вычитания (сложения), который, по моему мнению хорош, когда мы работаем с маленькими числами. Если его применять для сложения и вычитания любых смешанных чисел, то можно в результате получить «работу» с большими числами, что может привести к арифметическим ошибкам. Поэтому в видео его не рассматриваю. Применять можно, если ориентироваться, где и когда он будет рационален.
Просто и доступно о сложении смешанных чисел. Рассматриваем примеры на применение правила сложения смешанных чисел, при этом обращаем внимание на то, каким должен быть ответ, т.е. пример должен быть до конца решенным.
P.S. Есть второй способ вычитания (сложения), который, по моему мнению, хорош, когда мы работаем с маленькими числами. Если его применять для сложения и вычитания любых смешанных чисел, то можно в результате получить «работу» с большими числами, что может привести к арифметическим ошибкам. Поэтому в видео его не рассматриваю.
